大家在用chatgpt或者国内一些对标产品时，相信经常会遇见这种场景：模型一开始的回答结果并不如人意，用户对答案不满意时会继续进行交互，期望模型能输出更好的答案。

上述给的是一个比较好的例子，模型在用户反馈后真的自我更正输出了正确答案了。但有时候模型的新输出并未能比原来好多少，用户自己可能也不知道更好的答案是什么，跟一些所谓的领导一样只会否定但不给出有用的建议。那这种（适）自（应）我（p）纠（u）正（a）的能力要如何给到LLM呢？

在之前的文章 OpenAI o1的开源平替版self-replay RL来了！中，我们提到，光靠模型自己给自己打分，较难获得新的信息增量提升效果，要么需要多个模型，要么依赖于更高级的模型或其他形式的监督（如RAG提供外部输入）。但最强的那个模型要怎么继续进步呢？光靠模型自己反思真的不行吗？谷歌DeepMind团队提出多轮在线强化学习方法 SCoRe，完全使用自生成的数据进行训练，不需要任何外部反馈模型/信号，就能实现内在自我修正策略以“即时”修正自己的错误，提升了模型的推理能力。

我们理性的看，这种“自我反思”要有效果，有一个重要前提，是当前LLMs已经压缩了和问题答案相关的信息/知识，但还无法很灵活的使用，需要更高效的策略帮它提取&运用起来。

问题定义和建模

给定一个数据集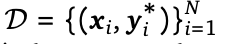，我们将训练一个LLM策略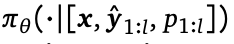，之前的模型l给出尝试性的回答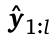，并结合一个辅助性的prompt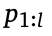（如让模型找错并提升回答质量），尽可能正确地解决问题x。这种形式类似multi-turn MDP。此外，训练时访问一个奖励函数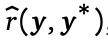，例如基于字符串匹配的答案检查功能，通过比较模型的输出和正确答案来评估正确性。模型学会了推断是否存在错误并进行修正，测试时就可以不需要奖励函数了。如图2所示。

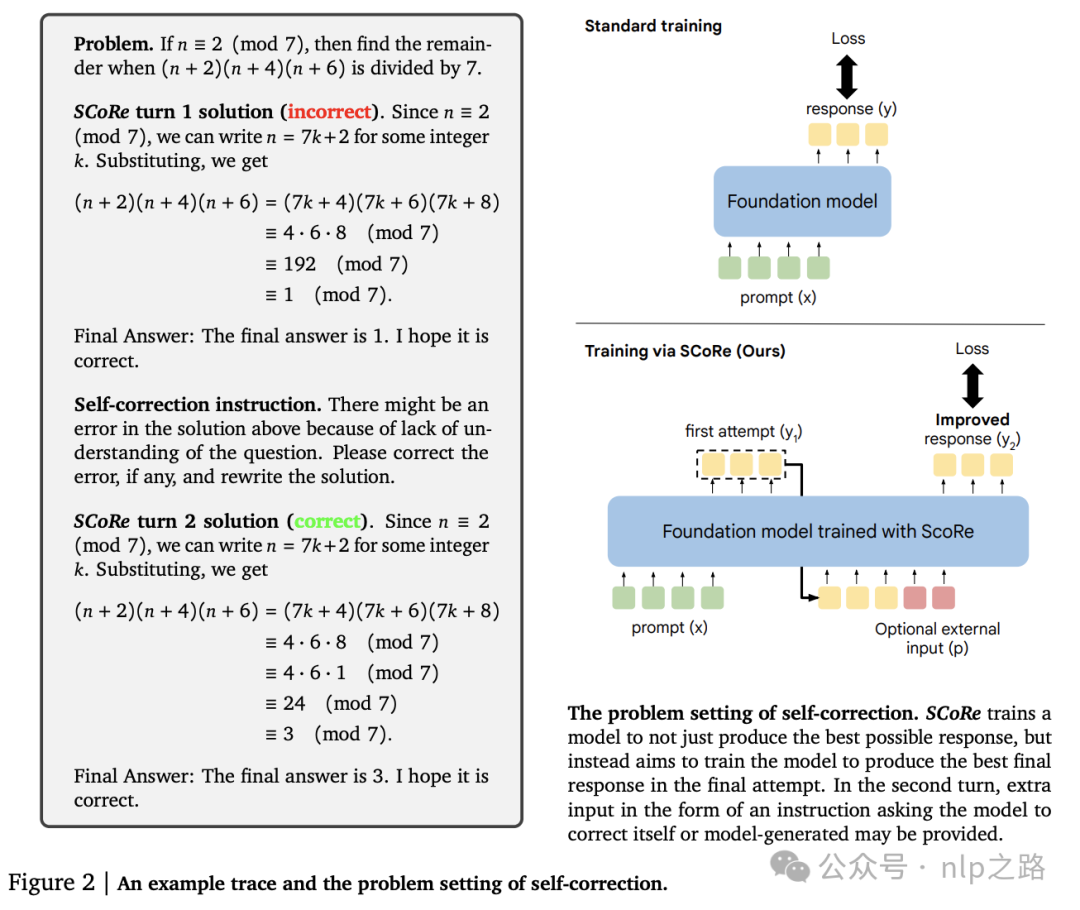
我们的目标是找到一种模型/策略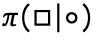，将一系列输入token ◦映射到一系列输出token □，以最大化在最后一轮结束时奖励函数给出的打分。可以建模为以下多步RL目标：

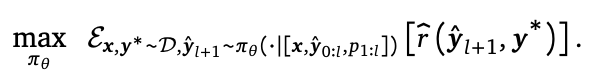
与直接让模型拟合标准答案的标准SFT或流行的RL微调不同，上述目标训练?同时进行多轮尝试，中间的输出间接的通过最终奖励优化，强迫模型思考并推理出正确答案，而非传统的sft那样通过maxlikelihood去“记忆”答案。类比我们中学学习数理化时，自己亲自动笔演算再去跟答案对比，学习/练习效果会好过光看题解不动手。

评估指标。为了衡量自我修正性能，定义以下指标：

（1）Accuracy@t1：模型在第一次尝试时的准确性；

（2）Accuracy@t2：模型在第二次尝试时的准确性，

（3）Δ(t1, t2)：第一次和第二次尝试之间模型准确性的净提高，衡量自我修正的有效性，

（4）Δi→c(t1, t2)：在第一次尝试中错误但在第二次尝试中正确的问题的比例，衡量自我修正可以解决多少新问题；

（5）Δc→i(t1, t2)：在第一次尝试中正确但在第二次尝试中错误的问题的比例，衡量模型能够理解响应正确的程度。

在自生成数据上进行监督式微调不足以实现自我修正

一种很容易想到的方法是利用从base模型收集的（prompt-错误答案-纠正prompt-正确答案）数据，通过某种形式的sft来训练自我修正。这种方案已经在单轮推理问题中显示出良好的扩展性。这样的SFT方法是否也对自我修正有效？

方法。提示现成的模型获得大量两轮自我修正轨迹。

STaR方法，过滤这些轨迹只保留成功修订错误响应的那些，并在结果数据集上运行SFT。

Pair-SFT，使用base模型构建正确和错误答案的集合，然后通过将错误答案与正确答案配对来生成“合成”修复轨迹。

数据集构建。MATH数据集上进行研究，并使用温度为1.0的Gemini 1.5 Flash提示生成自我修正轨迹。按照以下方式构建STaR和Pair-SFT的数据集：

（1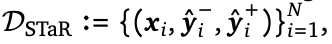）一次attempt中模型产生的正负例；

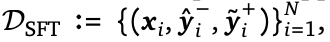
（2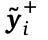）是从模型的一轮回答和二轮回答集中随机采样出的一个正确答案；

作者对这两个数据集进行了SFT。

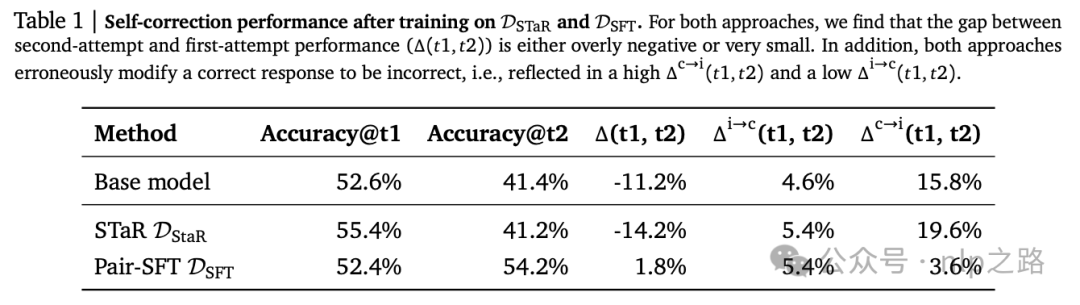
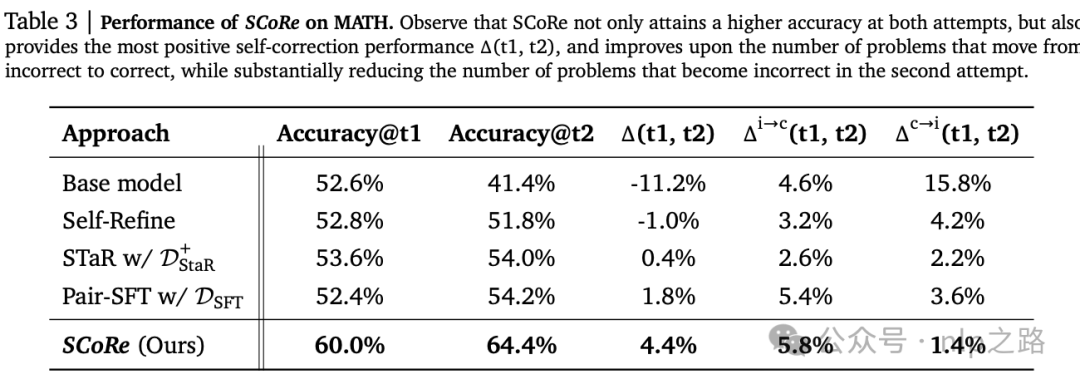
结果如上表所示。尽管Pair-SFT的Δ(t1, t2)相对于基础模型有大幅度提高，但进行自我修正几乎没有好处（1.8%的增益）。通过考虑Δi→c和Δc→i，SFT主要通过减少在修订后错误地将正确问题更改为不正确的问题的数量来提供帮助，并没有显著增加错误第一次尝试被正确修复的比例。这个结果与先前关于内在自我修正的研究一致，即Δ(t1, t2)可以忽略不计甚至为负。

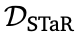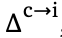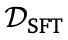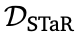与Pair-SFT不同，的训练并没有减少，这表明STaR策略并不清楚何时要修改，何时不修改。假设这种差异是由于和的数据分布：前者由于随机配对的性质，覆盖了更多样化的修正轨迹空间。观察到这一点，作者还训练了一个扩展版本的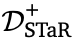和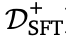，包含了更多的（正确-正确）元组，期望能防止模型错误地修改掉正确的答案，并且限制模型的改动幅度只能从一个正确响应修改为另一个正确响应。如下表所示。

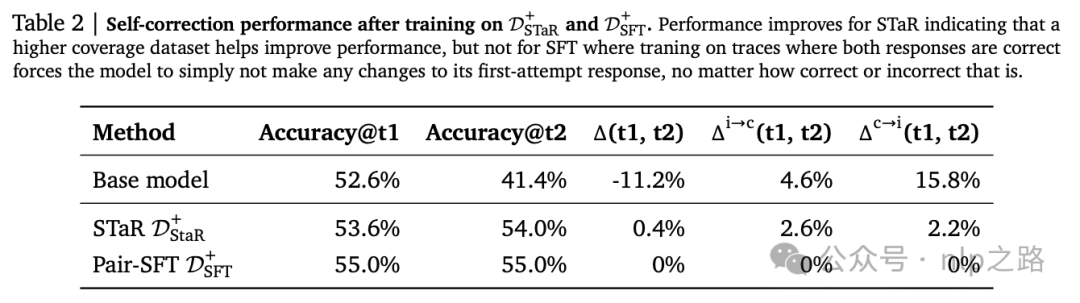
有趣的是，这样的数据对STaR和SFT有相反的效果：对于STaR，加入（正确-正确）数据有很大帮助，尽管Δ(t1, t2)还是基本无明显的正向提升。另一方面，对于SFT，包含这些数据放大了bias导致模型根本不改变其答案。

深入研究：分析自我修正行为。作者还可视化了STaR和SFT模型如何编辑它们的响应。特别是，测量了编辑距离比率，定义为响应之间的编辑距离与两个响应的总长度的比值，以总结模型修改其第一次尝试响应的程度。

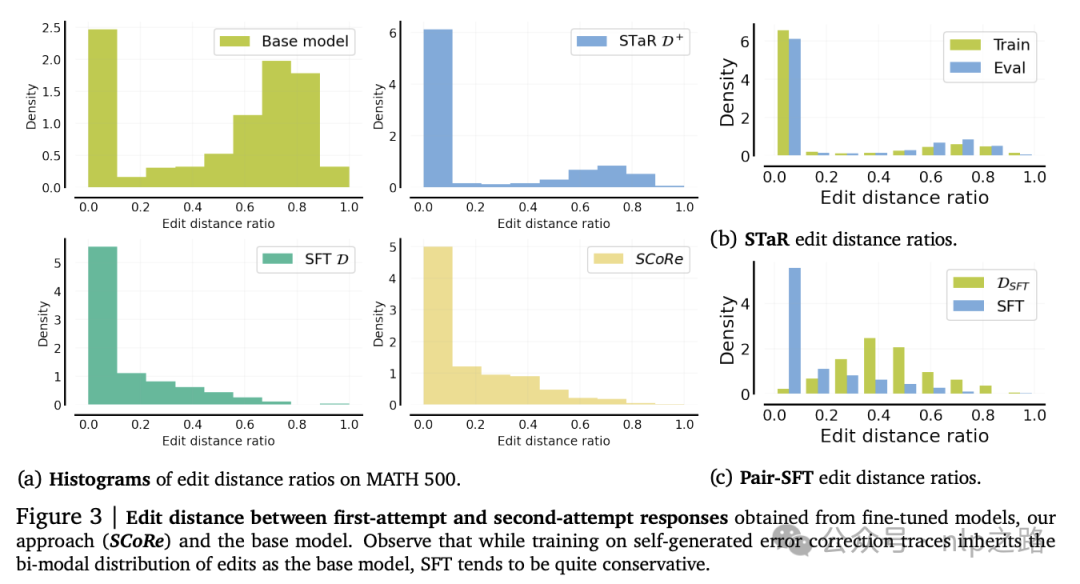
如图3a所示，base模型有时会对原始响应进行大幅度的修改，但经过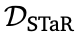和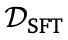微调的模型过于保守，通常根本不进行编辑。作者还绘制了在训练数据和STaR和Pair-SFT生成的自我修正轨迹中出现的编辑距离比率，并将其与训练和验证问题上的编辑距离比率进行了比较，如图3b和3c所示。虽然STaR在测试集上的泛化性基本跟训练集一致，但Pair-SFT在测试集的泛化不好。

看到Pair-SFT在训练和验证问题上的编辑距离比率之间的差异，我们还分析了SFT模型在固定集合的第一次尝试响应和自生成的第一次尝试响应上的自我修正准确性，如图4所示。

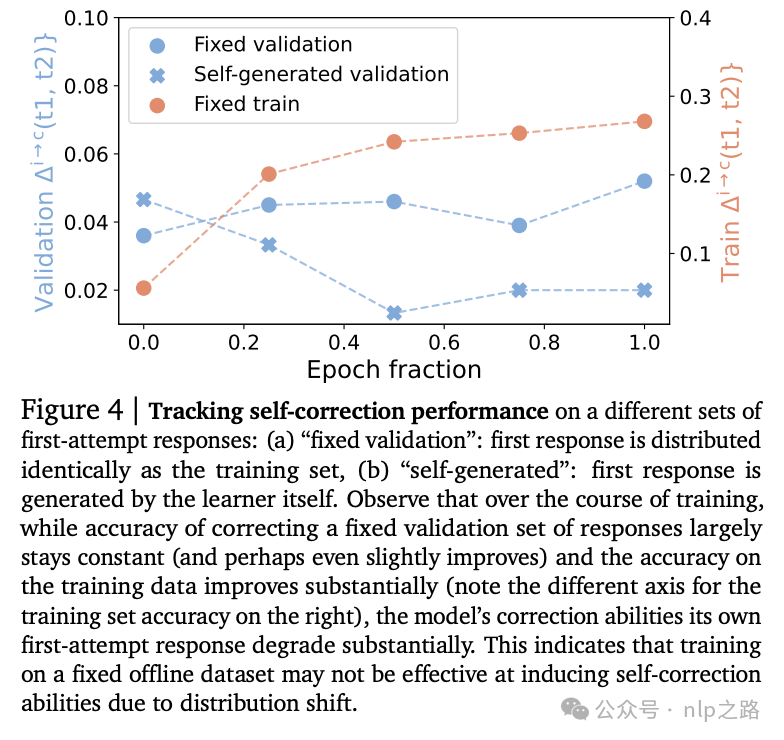
我们清楚地观察到训练与验证以及静态与自生成第一次尝试分布之间的不同行为：虽然该模型能够很好地优化训练修正准确性，并且也保持了在验证集中出现的第一次尝试的初始修正准确性（与训练分布独立同分布），但其自我修正准确性随着更多训练而降低。

教训：SFT的不足。我们展示了SFT方法的两种不同的失败源：STaR坚持只修正行为的一种模式，只进行微小更改，而Pair-SFT由于分布偏移，在具有更广泛覆盖的数据上训练导致在模型自身初始响应分布上的自我修正能力下降。这意味着有效的方法必须满足两个期望：

[D1]它应该直接在自生成的轨迹上训练，以缓解影响SFT的分布不匹配问题（图4）

[D2]所使用的自生成轨迹应该防止在学习过程中崩塌到进行微小编辑。

SCoRe：通过多轮强化学习自我修正

关键挑战。on-policy的多轮RL满足期望[D1]，解决了分布偏移问题，但是否也满足期望[D2]？作者运行了一个简单的多轮RL基线进行测试，发现尽管通过简单的多轮RL训练，每次尝试的性能随着训练有提高，但第二次尝试的性能与第一次尝试紧密耦合。随着训练的进行，标准的多轮rl趋于不改变其响应的偏见，导致没有自我修正能力。

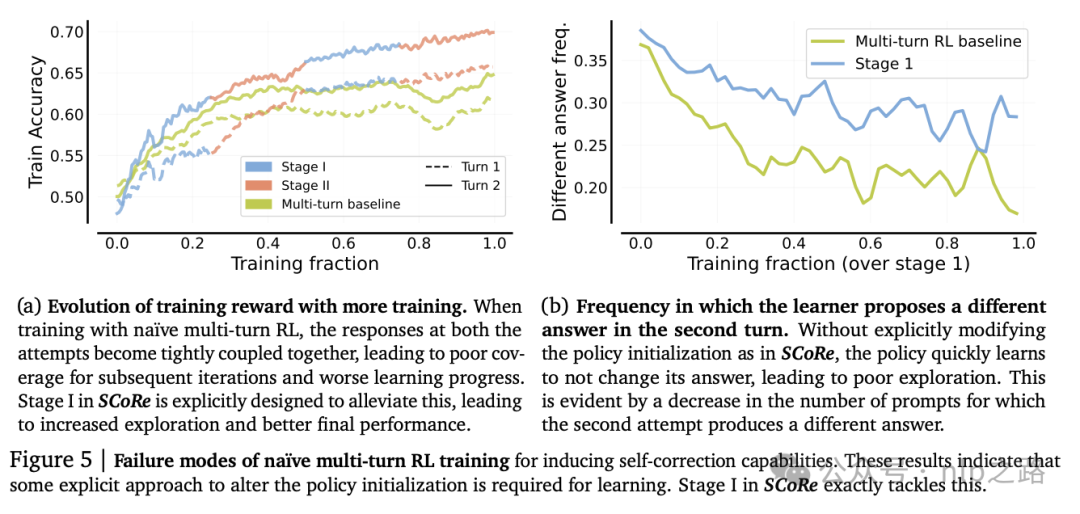
为什么会这样？优化RL策略时至少有两个同样好的解决方案：

（i）学习从第一次尝试到第二次尝试的改进策略

（ii）学习产生最佳的第一次尝试响应，然后在第二次尝试中不进行任何更正。

当然，只有前者的策略在新问题上泛化，也是我们更关心的问题，但过度参数化的LLM可能直接就学习（ii），因为在训练集上这两种策略看起来同样好。

抽象地说，在训练过程中学习“元策略”或自我修正策略是困难的，除非“直接”策略看起来不太可行。概念上，这与元学习中的记忆力挑战相似，它表明当提供相互排斥的任务时，few-shot meta-learning可能会恢复监督学习解决方案（不依赖于few-shot提供的额外上下文），直接预测输入的输出。

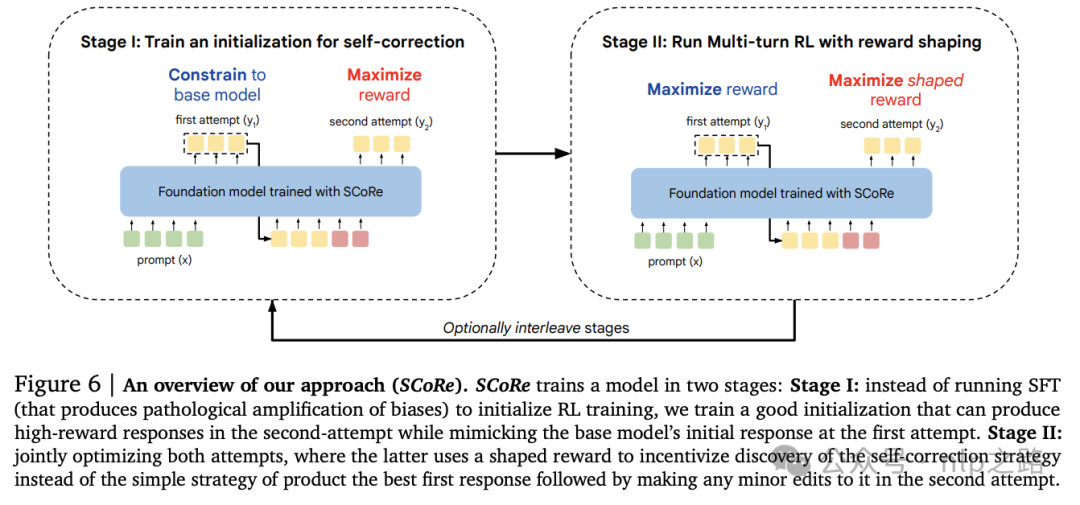
SCoRe旨在解决上述关键挑战。SCoRe分为两个阶段：

Stage I：SCoRe基于REINFORCE算法，通过明确鼓励模型在第二次尝试中产生高奖励修改，同时通过KL散度将第一次尝试响应分布约束为尽可能接近base模型，从而获得一个不易在后续RL中崩溃的良好初始化（不用SFT初始化）。

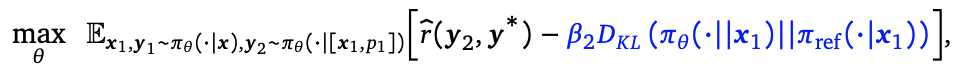
Stage II：我们使用Stage I的模型初始化运行多轮RL。为了使学习偏向于学习（i）而非（ii），我们通过reward shaping来偏置学习过程：从第一次尝试到第二次尝试，如果正确性有更大的改进，则提供更高的奖励，引导模型积极学习自我修正解决方案。用policy gradient算法优化。同样，与上一轮的策略增加KL散度保证模型稳定性。

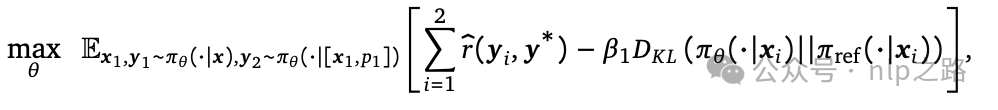
具体来说，给定两轮策略梯度轨迹 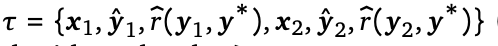，其中第二轮尝试的奖励函数在第一轮的基础上多加了一项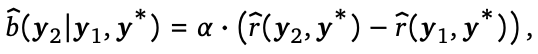系数一般远大于1，当模型第二轮尝试正确性比第一轮有提高，则reward为正，正确性降低，则reward为负，用于鼓励模型学习自我修正的策略。这相当于对模型的训练过程添加了正则项，逼迫模型学习怎么提高准确性的策略，而不是光“记忆”训练集答案，实现更好的泛化性。

SCoRe以交错方式应用第一阶段和第二阶段多次迭代。我们对所有实验使用小?1，并发现设置 ?2 = 10?1 在我们的实验中足够好。实际上，也可以使用自适应 ?2，试图平衡第一次尝试的KL正则化和第二次尝试策略损失的大小。在我们的一些实验中，我们还选择通过在RL中重复抽样base模型获得的第一次尝试解决方案，来扩大用于策略RL的状态覆盖范围。我们发现，特别是在第二阶段，当第一轮策略可能已经从基础模型进一步偏离时，合并这些数据，尤其是当尝试从有限数据中学习时，很有用。

在MATH数据集上进行了消融实验。旨在回答以下问题：

（1）多轮训练的重要性：RL训练以最大化单轮性能能否实现更好的Accuracy@t1或Accuracy@t2？；

（2）多阶段训练的重要性：第一阶段对SCoRe有多重要？换句话说，为什么不直接运行第二阶段？；

（3）reward shaping的影响。如果假设第一阶段完全相同，那么在第二阶段移除reward shaping项会如何影响SCoRe的性能？；

（4）策略RL的重要性。如果我们在第二阶段用STaR替换REINFORCE会怎么样？

所有这些消融实验的结果如表5所示。

（1）单轮训练提高了第一轮的性能，但Δ(t1, t2)为负。

（2）第一阶段对SCoRe至关重要；没有它，模型实现了2%较低的Δ(t1, t2)和3%较低的accuracy@t2。

（3）我们发现移除reward shaping也会损害性能，这表明两个阶段的RL目标在教授自我修正行为方面都发挥了重要作用。

（4）用STaR替换第二阶段的REINFORCE会导致显著较低的绝对性能，并且没有明显的改进自我改进性能，这与Havrilla et al. (2024a)的发现形成对比，即STaR和on-policy RL在单轮RL中具有相似的收敛速率。这表明在自我修正这个场景中利用策略样本尤为重要。

推理计算扩展与自我修正

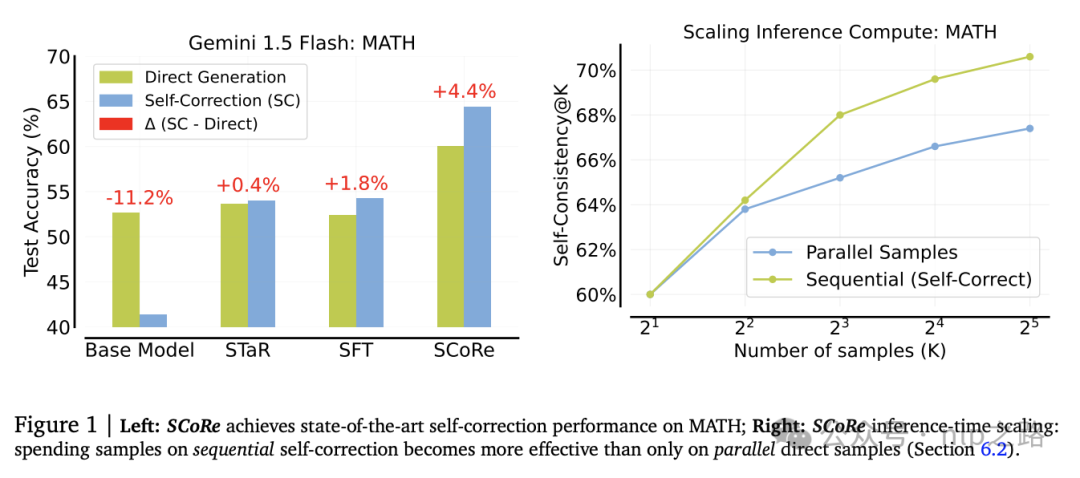
作者还研究了SCoRe是否可以与推理时计算扩展策略结合使用。为此，测试了自我一致性解码，也称为多数投票，即采样一组多样化的解决方案，然后从这些解决方案中选择一致性最高的答案。通常，默认策略是并行采样所有解决方案以执行多数投票。如图1（右），与其并行采样2K个解决方案，不如先并行采样K个解决方案，然后对每个解决方案执行一轮自我修正。在每个问题的32个解决方案中，平行采样显示了7.4%的准确性增益，而结合使用自我修正的顺序采样产生了10.5%的增益。

SCoRe的定性分析

我们还对SCoRe如何解决基础LLMs的自我修复缺陷进行了定性研究，发现SCoRe能够以多种方式完善自己的响应 - 在必要时重写整个解决方案，或者复制解决方案的正确部分，同时修正错误的部分。对于后者，我们有趣的发现SCoRe特别擅长修正其计算错误，甚至表现出一种偏见，即在某些计算和操作中展示更多的步骤，以增加产生正确答案的可能性（谷歌也发现了推理阶段的scaling law）。

附录：

《Training Language Models to Self-Correct via Reinforcement Learning》

https://arxiv.org/pdf/2409.12917