少样本学习(Few-Shot Learning,FSL)是机器学习领域中的一种重要技术,其目标是在仅使用少量样本(例如50个或更少)的情况下,设计出能够高效学习和准确预测的机器学习模型。这种技术在许多应用领域都具有重要的实际意义,例如在数据标注成本较高的场景中,或者在面对快速变化的任务时。应用包括图像分类、情感分类和对象识别。
理论基础
少样本学习(Few-Shot Learning,FSL)的理论基础有三个角度:贝叶斯、信息论和优化。
从贝叶斯的角度来看,它涉及到利用先验知识来提高学习性能。在FSL中,这意味着将关于任务或领域的先验知识纳入模型中,以帮助模型更好地从一个小数据集中泛化。贝叶斯方法还可以帮助进行模型选择和超参数调整。
从信息论的角度来看,它关注量化从小数据集中学习所需的信息量。在FSL中,这意味着找到从一个小数据集中提取最有用信息的方法来提高学习性能。信息论还可以帮助设计更好的数据增强技术和选择最有信息量的样本进行训练。
从优化的角度来看,它涉及到找到可以最小化损失函数的最佳模型参数。在FSL中,这意味着找到能够从小数据集中泛化良好的最佳模型。优化方法还可以帮助设计更好的元学习算法和选择最适合FSL的优化算法。
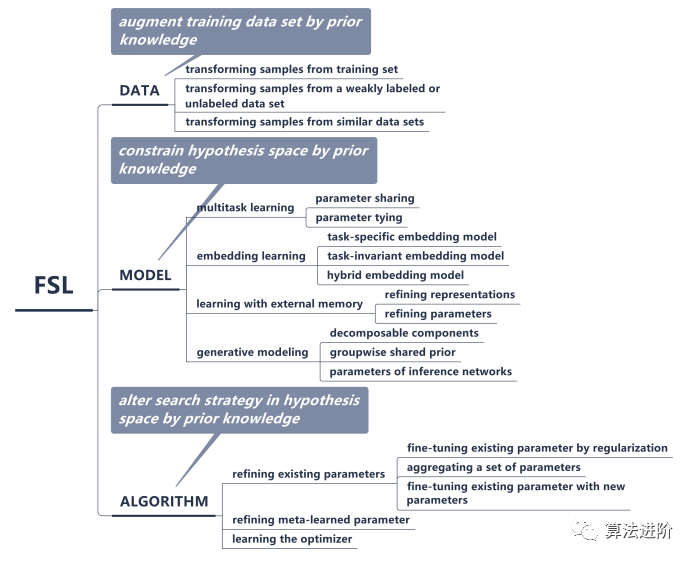
弱监督学习。与FSL类似,弱监督学习也是从有限的标记样本中学习,但是标记的质量比FSL更低。弱监督学习通常使用一些弱标记来代替精确标记,例如图像级标记、区域级标记等。不平衡学习。不平衡学习是指在训练数据中,不同类别的样本数量存在较大差异的情况。不平衡学习通常使用一些采样策略或代价敏感学习来解决这个问题。迁移学习。迁移学习是指将已学习的知识或模型应用到新的任务或领域中。迁移学习通常使用一些领域自适应或知识迁移的方法来实现。元学习。元学习是指学习如何学习的过程。元学习通常使用一些元学习算法来学习如何快速适应新的任务或领域。元学习可以被看作是FSL的一种特殊情况,因为FSL也是从有限的样本中学习如何快速适应新的任务。总之,FSL与这些相关学习问题有一些相似之处,但也有一些不同之处。FSL的独特之处在于它专注于从极少量的标记样本中学习新的任务或概念,而其他相关学习问题则更关注FSL的核心问题是经验风险最小化器并不可。基于如何使用先验知识来处理这一核心问题,我们将FSL方法从三个角度进行分类:(a) 数据,增强了FSL的监督经验;(b) 模型,将FSL的假设空间限制为更小;(c) 算法,则改变了在给定假设空间中寻找最佳假设的搜索策略。如图1,2所示:
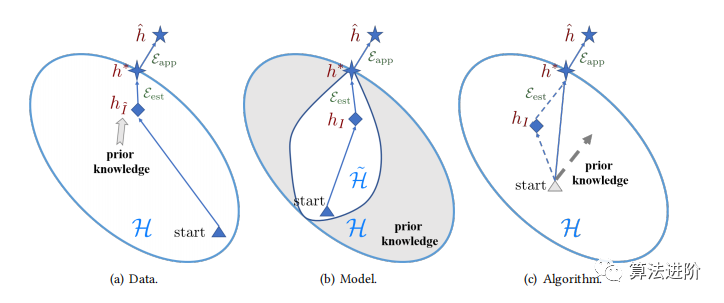 图1 关于FSL方法如何解决少样本问题的不同分类
图1 关于FSL方法如何解决少样本问题的不同分类
使用先验知识扩充数据Dtrain,以提高监督信息的丰富度,可从增广的样本集中获得可靠的上手标注,如图2。通过手工制定的规则进行数据扩充,可以引入不同种类的模型不变量,但需要昂贵的劳动力成本。此外,这些规则可能特定于数据集,难以应用于其他数据集。因此,手动数据扩充无法完全解决FSL问题。除了手工制定的规则,我们根据哪些样本被转换并添加到Dtrain,将更先进的数据扩充方法归类为表1所示。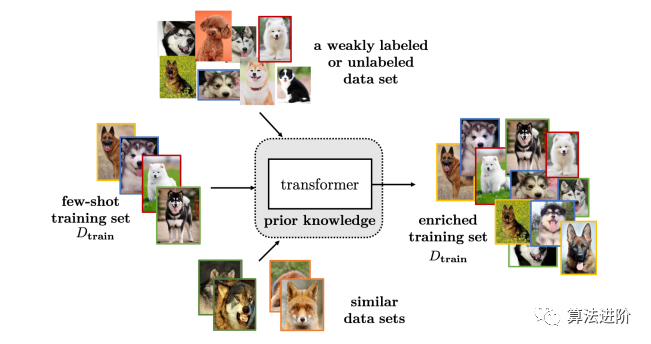
表1 基于数据视角的FSL方法的特征。变换器t(·)接受输入(x,y)并返回合成的样本( ˜x, ˜y)以增强少样本Dtrain。
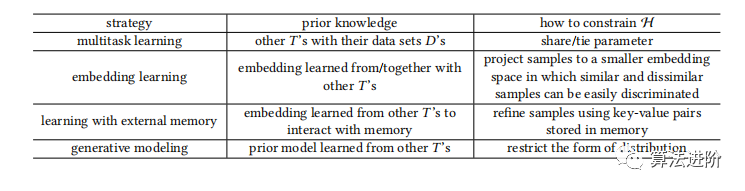
扩增策略的选择取决于应用程序,有时需要少数样本学习。可以通过从弱标记或未标记数据集中转换样本进行扩增,或从相似的类中转换样本。如果只有已学习的转换器可用,可以通过从Dtrain转换原始样本进行扩增。扩增策略可能针对每个数据集定制,不易应用于其他数据集。为了逼近真实世界假设,模型需确定一个包含假设家族h的假设空间H,以减小最优h*与^h间的距离。有限样本数下,可只选包含简单模型的小H。但现实问题复杂,一个小的H中的假设h可能无法很好表示,导致Eapp(H)很大。因此,FSL更倾向于足够大的H,但会使标准机器学习模型变得不可行。FSL方法利用先验知识E将H限制在较小的˜ H中以学习,降低经验风险最小化器过拟合的风险。该类方法可根据不同先验知识分为四种类型(表2)。表2 基于模型视角的FSL方法的特征
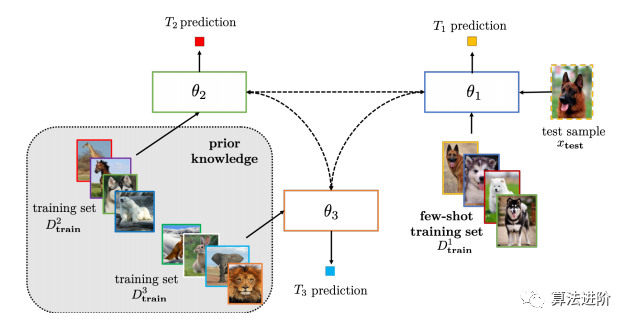
 多任务学习、嵌入学习方法、记忆网络和生成模型都是解决少数样本学习的方法。多任务学习需要所有任务一起训练,新任务到来时需重新训练整个模型,如图4,5。
多任务学习、嵌入学习方法、记忆网络和生成模型都是解决少数样本学习的方法。多任务学习需要所有任务一起训练,新任务到来时需重新训练整个模型,如图4,5。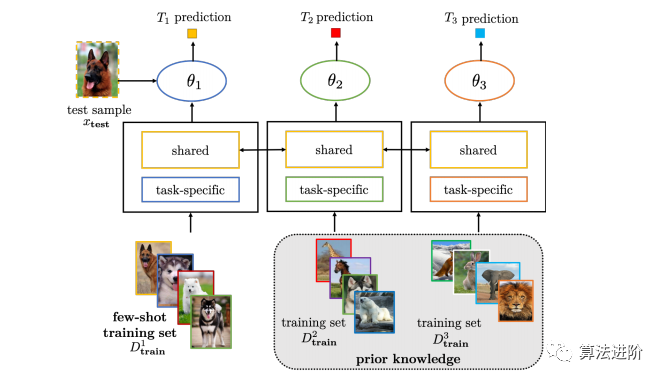
嵌入学习方法适用于大规模数据集,但当任务不相关时可能效果不佳,如图6,7。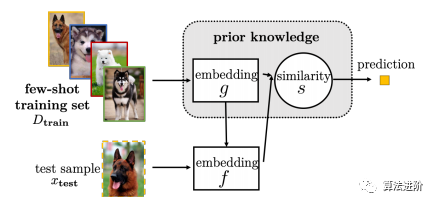
记忆网络通过训练简单模型保护内存插槽,但会带来空间和计算成本,如图8。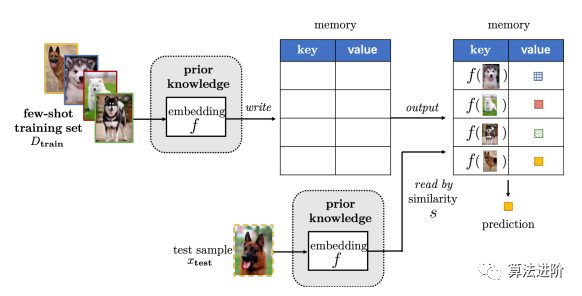
生成模型从概率分布中学习先验知识,可减小H,但推断成本高,如图9。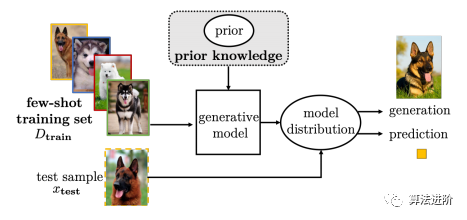
该算法是在假设空间H中搜索参数θ的最佳假设h*的策略。在监督信息丰富且训练样本足够的情况下,更新参数θ和交叉验证可得到合适步长α。但FSL中训练集Dtrain样本少,经验风险最小化者可靠性低。表3为三种使用先验知识影响θ获取方式的方法:表3 基于算法视角的FSL方法特性
 (1)细化现有参数,从其他任务中学习初始参数θ0,然后使用Dtrain进行细化,如图10-12所示:
(1)细化现有参数,从其他任务中学习初始参数θ0,然后使用Dtrain进行细化,如图10-12所示: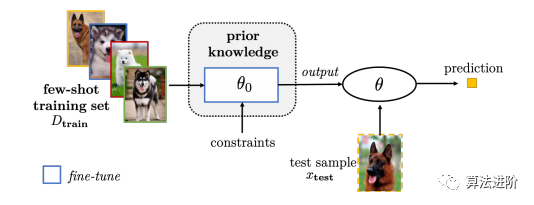
图10 通过正则化对现有参数θ0进行微调来解决FSL问题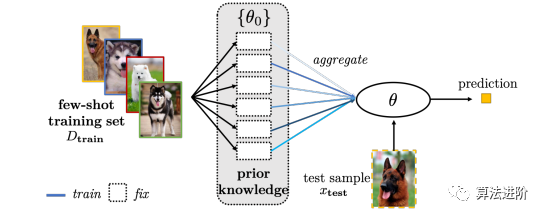
图11 通过将一组参数θ0聚合到θ来解决FSL问题。给定一组预先训练好的θ0,只需要学习组合权重(蓝色线条)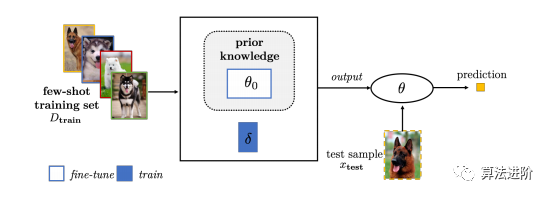
图12 通过微调现有的参数θ0,引入新的参数来解决FSL问题(2)细化元学习参数,从与少样本任务相同的任务分布中元学习初始参数θ0,然后由学习者使用Dtrain进一步细化,如图13所示: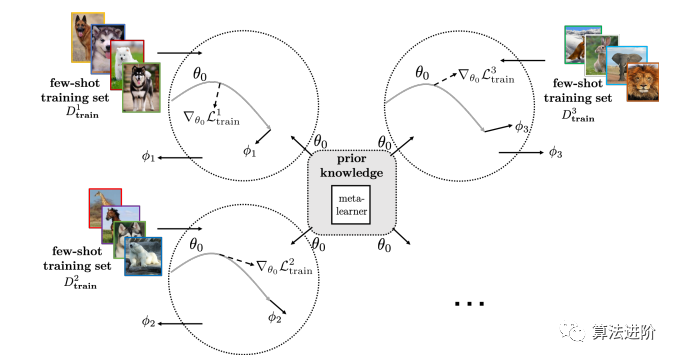
(3)学习优化器,该策略学习一个元学习器作为优化器,为每个学习者直接输出搜索步骤,例如改变搜索方向或步长,如图14所示: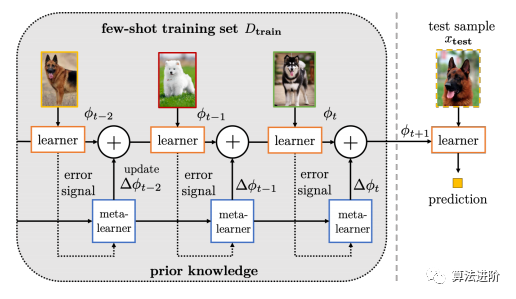
另外,通过元学习,可以借助提供的数据集和元学习者所提取的跨任务元知识来改善新任务T的概率P(如图15所示)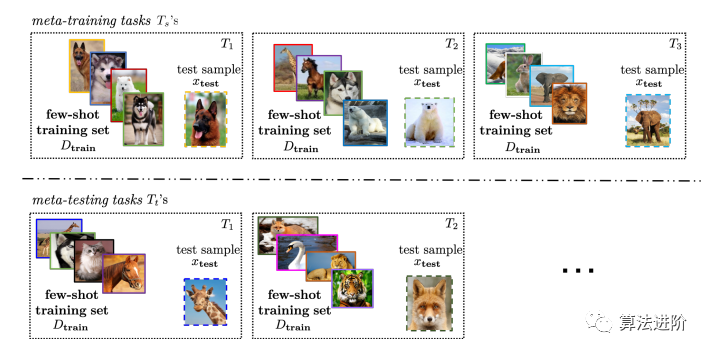
少样本学习方法主要可以分为三类:基于非情景的方法、基于元学习的方法和基于度量学习的方法。基于非情景的方法(Non-Metric Methods)这种方法主要依赖于从大量未标记的数据中提取信息,并利用这些信息对新的样本进行分类或回归等任务,依赖于整个数据集的统计性质,而非依赖于特定的样本。它通常包括k近邻(k-NN)方法和贝叶斯方法等。在非情景的方法中,模型并不关注特定样本的信息,而是更关注整个数据集的信息。这种方法通常利用一些常见的统计方法,例如聚类、主成分分析等来从大量未标记的数据中提取有用的信息,然后利用这些信息来完成新的样本的分类或回归等任务。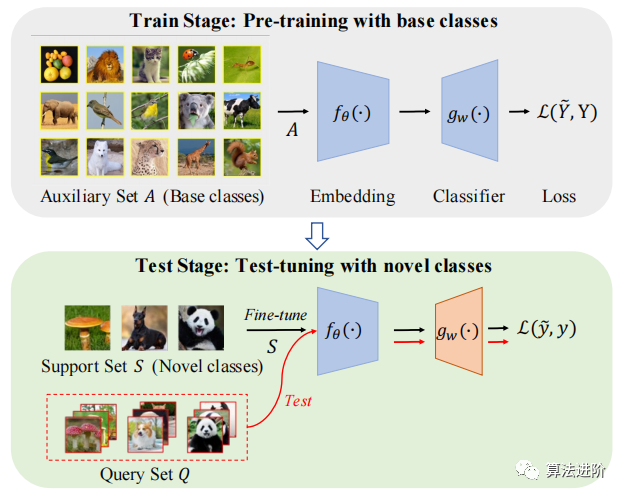
元学习是一种特殊类型的机器学习方法,它的目标是使得模型能够在接触到新的任务时快速学习和适应。因此,元学习可以被认为是一种在学习如何学习的过程中进行学习的机器学习方法。其中,模型学习通常被分为两个阶段:元训练阶段和元测试阶段。在元训练阶段,模型会接触到大量不同的学习任务,并学习如何快速适应这些任务;在元测试阶段,模型会接触到新的任务,并利用在元训练阶段学到的知识来快速适应这些新任务。元学习的主要目标是在接触到新的任务时,通过利用之前学到的知识和经验来快速适应和学习新的任务。这种方法通常利用一些常见的算法和技术,例如神经网络、强化学习等来学习如何快速适应和学习新的任务。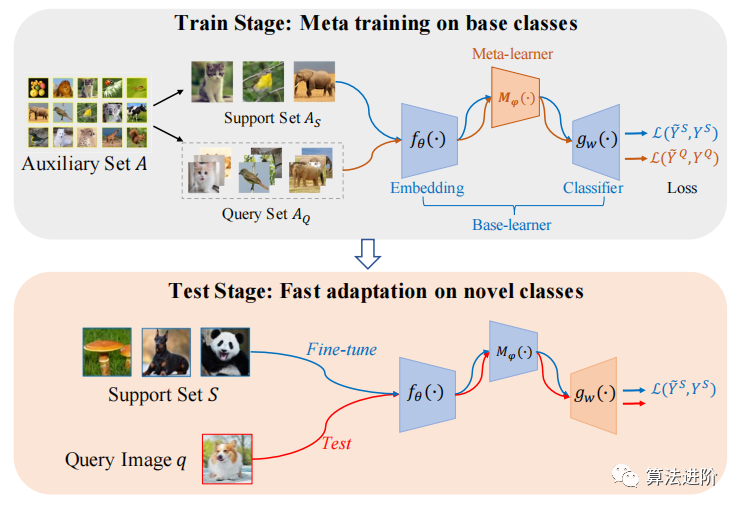
基于度量学习的方法(Metric Learning)度量学习方法是一种通过学习数据间的相似性关系来进行学习的机器学习方法。它的目标是学习一个度量空间,这个度量空间可以对输入数据的相似性进行准确的衡量。常用的度量学习方法包括Siamese网络、对比学习和三元组损失等。Siamese网络是一种通过学习一个共享的嵌入空间来对输入数据进行表示的方法。这个嵌入空间可以将输入数据映射到同一个向量空间中,使得同类样本的向量距离更近,而异类样本的向量距离更远。对比学习是一种通过最大化两个样本之间的相似性或者最小化两个样本之间的不相似性来进行学习的学习方法。三元组损失是一种通过最小化一个样本与同类样本之间的距离和与异类样本之间的距离之差来进行学习的学习方法。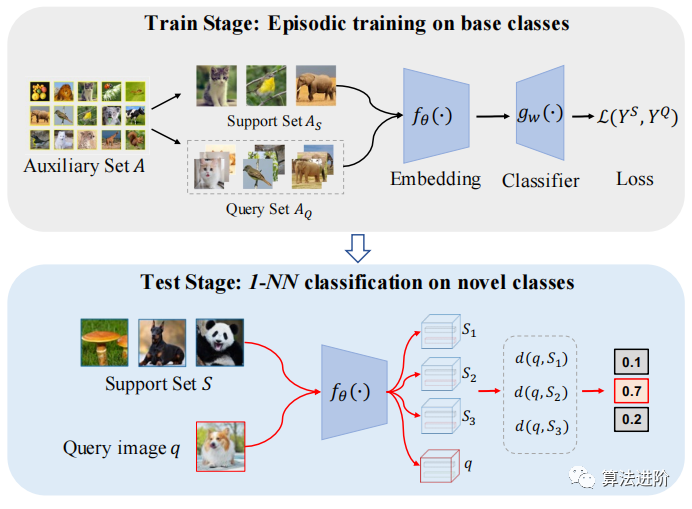
总的来说,少样本学习方法在面对只有少量数据标注的情况下具有非常重要的作用,它能够有效地利用未标注数据进行训练,从而提高模型的泛化能力和预测准确性。现有的大多数研究都在计算机视觉领域的FSL问题上进行,其中最受欢迎的两个应用是字符识别和图像分类。最近,一个由多个图像数据源构建的大型多样化的基准数据集被提出,并考虑了其他图像应用,包括对象识别、字体样式转换、短语接地、图像检索、对象跟踪、特定对象计数、场景位置识别、手势识别、部分标签、图像生成、跨域的图像翻译、3D对象的形状视图重建以及图像字幕和视觉问答。此外,FSL也被成功应用于视频应用,包括运动预测、视频分类、动作定位、人员再识别、事件检测和对象分割。FSL的使用在自然语言处理的应用包括解析、翻译、句子完成(使用从提供的集合中选择的单词填充空白)、从短评中分类情感、对话系统中分类用户意图、刑事指控预测、诸如nonce定义之类的单词相似性任务和多标签文本分类。最近,FewRel的新关系分类数据集的发布弥补了自然语言处理中FSL任务缺乏基准数据集的不足。声学信号处理在语音识别和合成方面取得了进展。从用户音频样本中克隆声音,这可以在地图应用程序中生成个人语音导航,或在智能家居工具包中模仿父母的声音来给孩子讲故事。近期,一次性声音或文本样本可实现用户间和跨语言的语音转换。医学领域的少样本药物发现,以及一次性架构搜索(OAS)在深度网络学习中的应用,需一次训练超级网络就可以找到良好的架构。此外,FSL也被用于曲线拟合以及通过逻辑推理来理解数字类比以执行计算。LibFewShot(https://github.com/rl-vig/libfewshot)是一个用于少样本学习的开源库,它提供了一个统一框架来实现和比较各种少样本学习方法,代码简洁、结构明了,易于新接触小样本学习的新手学习使用。该库使用PyTorch实现,包括多种最先进的少样本学习方法。此外,它还提供了用于数据加载、模型训练以及在多个基准测试上评估各种主干网络架构的工具,
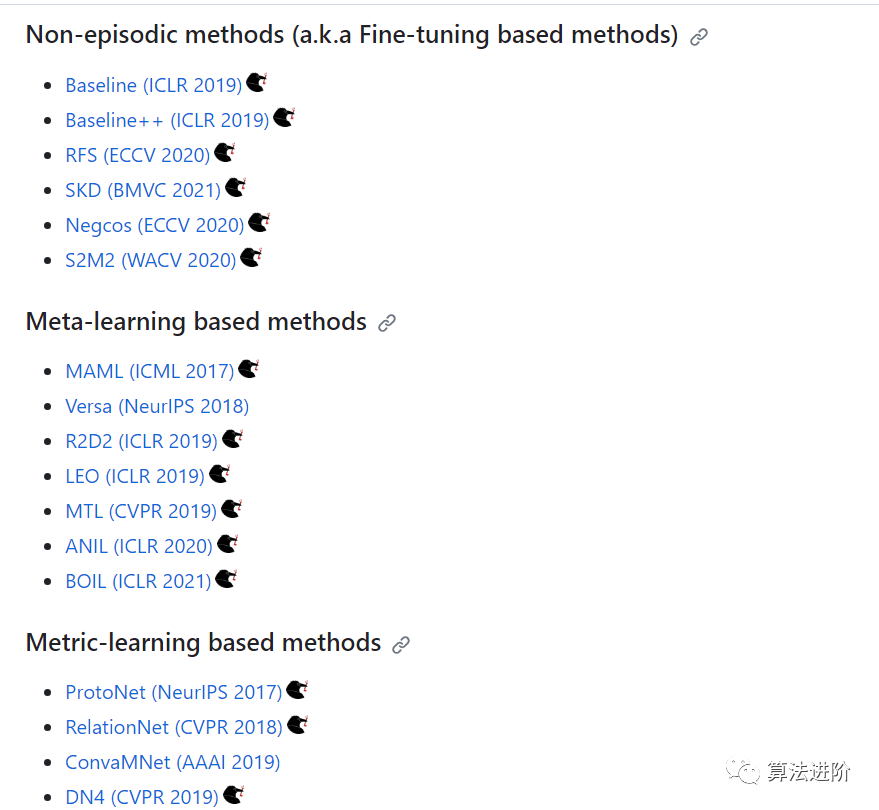
LibFewShot 实现了 17 个具有代表性的算法,从上到下依次是基于微调的方法、基于元学习的方法和基于度量的方法,复现结果如下:
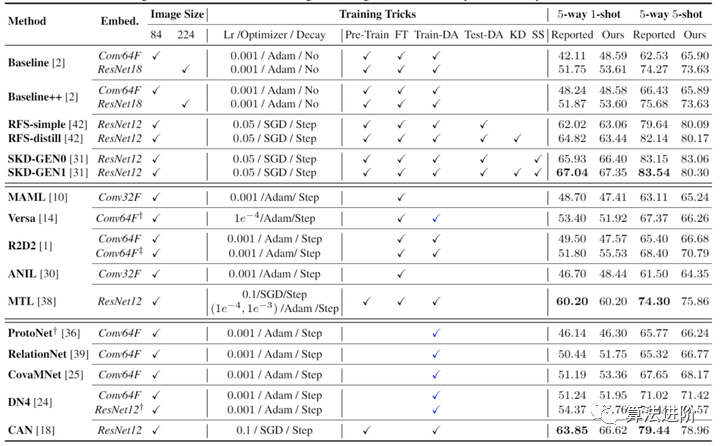
图1 关于FSL方法如何解决少样本问题的不同分类
