MSQA和哈佛发表rStar,对标OpenAI的超级对齐Q*项目!
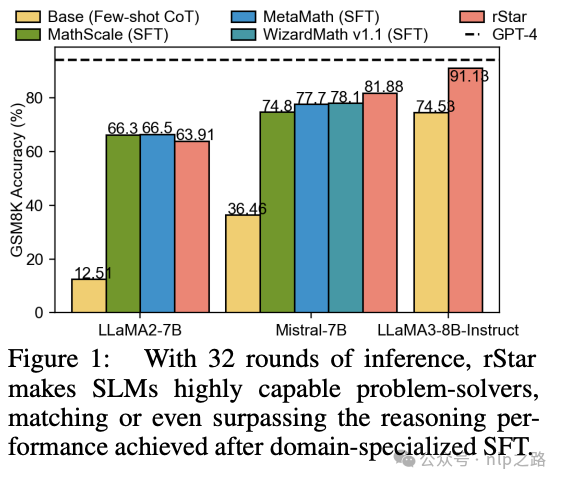
摘要:本文介绍了一种名为rStar的self-play互推理方法,它显著提高了小型语言模型(SLMs)的推理能力,而无需微调或更高级的模型。首先,目标SLM通过丰富的类人推理动作来增强蒙特卡洛树搜索(MCTS),构建更高质量的推理轨迹。接下来,另一个能力与目标SLM相似的SLM充当判别器,验证目标SLM生成的每个轨迹。得分都很高的推理轨迹被认为是相互一致的,因此更有可能是正确的。在五个SLMs上的实验表明,rStar可以有效解决多种推理问题,包括GSM8K、GSM-Hard、MATH、SVAMP和StrategyQA。引人注目的是,rStar将LLaMA2-7B在GSM8K数据集上的准确率从12.51%提高到63.91%,将Mistral-7B的准确率从36.46%提高到81.88%,将LLaMA3-8BInstruct的准确率从74.53%提高到91.13%。
1 引言
大型语言模型(LLMs)目前在复杂推理方面效果还不是太好。例如,像Mistral-7B这样的最先进模型即使使用了思维链(CoT)等技术,在GSM8K数据集上只能达到36.5%的准确率。尽管微调被证明是提高推理能力的有效方法,但大多数LLMs依赖更高级模型(如GPT-4)合成或提取的微调数据。与此同时,业界一直在探索一种互补且更具挑战性的方法:在没有教师LLM(包括人工专家标注更多数据,以及借助更好的LLM模型做知识蒸馏)的情况下改进推理。
一种有前景的范式是在没有高级模型的情况下利用LLMs自身的知识来提高推理能力。例如,自探索(Self-Exploration, RAP,《Reasoning with Language Model is
Planning with World Model》https://arxiv.org/pdf/2305.14992v1)方法通过自我奖励的反馈迭代地提高LLMs的推理性能。然而,研究表明,这种范式通常存在两个基本问题。首先,LLMs在推理过程中通常很难有效地探索解决方案空间。自我探索往往会陷入低质量推理步骤的解决方案空间,即使经过多次尝试也是如此。例如,我们的实验表明,在GSM8K上使用RAP进行32轮自我探索后,LLaMA2-7B生成的正确轨迹只有24%。其次,即使自我探索能够找到高质量的推理步骤,SLMs也很难判断哪些推理步骤质量更高或确定哪个最终答案是正确的,因此很难有效地指导自我探索。我们的研究表明,基于简单奖励的自我探索引导可能并不比随机猜测更好。
上述两个问题在更小型的LLMs(即SLMs)中更加明显,因为它们的性能更弱。例如,虽然GPT-4可以通过自我提炼其输出来提高性能,但在SLMs中这些方法的效果较差,甚至可能导致性能下降。
本文介绍了一种名为自博弈相互推理(Self-play muTuAl Reasoning, rStar)的新方法,它在无需微调或高级模型的情况下,在推理期间显著提高了SLMs的推理能力。为了应对前述挑战,rStar将推理分解为自博弈相互生成-判别过程,如图2所示。
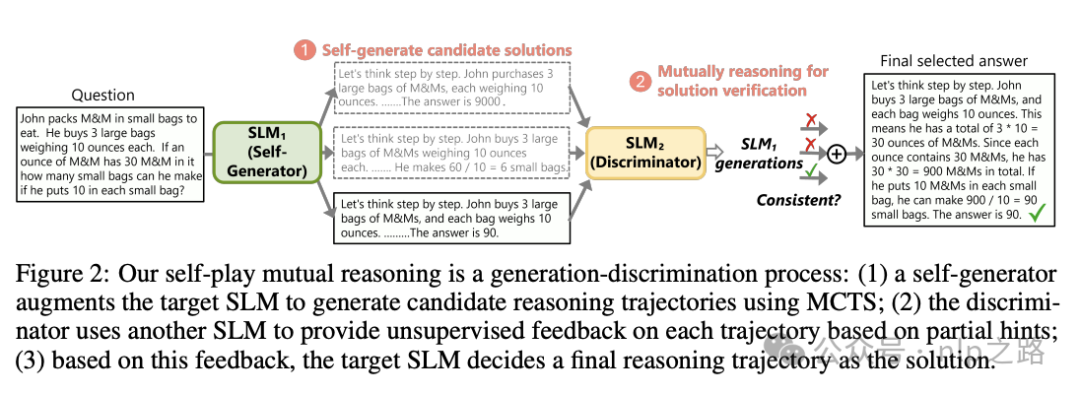
rStar针对上述两个问题提出的解法如下:
尽管依赖传统的蒙特卡洛树搜索(Monte Carlo Tree Search, MCTS)让SLMs自我生成推理步骤,但rStar提倡在自我探索中使用更丰富的推理动作集。新提出的动作模拟了给定当前推理状态下的人类推理行为,例如分解和搜索特定的推理步骤,提出新的子问题,或重新表述给定问题。这使得SLMs能够在自我探索中生成高质量的候选推理轨迹。
为了有效地指导生成的推理轨迹之间的探索,rStar通过称为相互一致性的新判别过程增强了MCTS过程。具体来说,rStar使用第二个能力相似的SLM作为判别器,为MCTS生成的每个候选推理轨迹提供无监督的反馈。为了提高反馈的准确性,rStar向第二个SLM提供采样的部分推理轨迹作为提示,要求其完成剩余的推理步骤。rStar认为相互同意的推理轨迹质量更高。相互一致性反映了在缺乏监督的情况下的常见人类实践,其中同行(即两个SLMs)对推导出的答案的一致性表明了更高的可能性是正确的。因此,相互一致性提供了比其他方法(如自我一致性)更有效的跨任务推理,并避免了训练奖励模型时过度拟合特定任务的风险(类似model ensemble)。
通过在五个SLMs和五个多样化推理任务上的广泛实验,我们证明了rStar的有效性。仅通过32轮MCTS推理,rStar就显著增强了SLMs的推理能力,与微调基本持平甚至超过了微调后的准确率。例如,rStar将LLaMA2-7B在GSM8K数据集上的准确率从12.51%提高到63.91%,将Mistral的准确率从36.46%提高到81.88%,将LLaMA3-8B的准确率从47.23%提高到85.52%。此外,我们进行了全面的实验来验证rStar相对于最先进基线的优越性,包括单轮推理技术(如少数样本CoT)、多轮提示方法(如自我一致性)和自我改进技术(如RAP、ToT、自我评估和自我验证)。
2 相关工作
提示语言模型进行推理:基于提示的方法,如链式思考(Chain-of-Thought, CoT),专注于设计指令和pipeline来增强LLM在推理期间的表现。最近的进展包括规划、问题分解、抽象、编程。旨在提高单轮推理性能,并且与本文的方法没有冲突,可叠加使用。
LLM自我改进:基于微调的方法利用预训练的LLM的能力来合成数据,并逐步提高其性能。高级提示技术,如自我验证和RAP,通过基于推理时自我诊断的反馈进行迭代自我探索来提高性能。然而,所达到的性能往往取决于LLM的固有能力,对于SLM来说,它们较弱的指令遵循能力和不可靠的自我奖励可能会误导自我改进。
采样推理路径:最近的工作在数学推理方面表明,采样多样化推理路径与贪心一次性解码相比,可以显著提高性能。自我一致性(Self-Consistency, SC)每次只采样一个完整的CoT路径。树搜索方法,如MCTS,通过分解任务并采样更简单、个别的中间推理步骤来进一步提高性能。然而,大多数方法的动作空间有限。例如,RAP仅分解子问题,而AlphaMath仅搜索一个CoT步骤,限制了在生成更好轨迹方面的有效性。
答案验证:为了选择正确的推理轨迹,多数投票是一种广泛使用的方法。为了提高准确性,一些研究训练价值模型或奖励模型进行验证,但需额外的标注成本并有过拟合特定任务的风险。自我验证利用LLM的能力进行反向自我验证。然而,其有效性取决于其固有的有效推理能力。最近的研究表明,LLM很难在仅依靠自我评估并在没有任何外部反馈的情况下纠正其初始响应(别做梦了,左脚踩右脚是上不了天的)如下表,自我评估的reward换成随机reward效果差不多

这些相关工作展示了当前领域内对提高语言模型推理能力的不同研究方向,包括通过提示、自我改进、路径采样和答案验证等方法。论文提出的rStar方法在这些现有研究的基础上,通过自博弈相互推理机制,进一步推动了小型语言模型在推理任务上的性能。
3 方法论
3.1 概述
问题表述:为了通过SLMs解决推理问题,我们将其表述为一个多步推理生成任务,将问题分解为更简单的子任务。这比传统的基于链式思考(Chain-of-Thought, CoT)的推理方法更有效,因为对于SLMs来说,正确生成单个步骤比在单次推理中完成所有推理步骤要容易得多。我们利用蒙特卡洛树搜索(Monte Carlo Tree Search, MCTS)算法来增强目标SLM进行自我生成多步推理解决方案。
挑战:MCTS允许SLM探索和评估多个潜在的解决方案。理想情况下,通过平衡新可能性的探索与高回报动作的利用,SLM可以逐渐完善其推理步骤,以生成最终正确的推理轨迹。然而,由于SLM的能力有限,传统的MCTS带来的改进很小。首先,庞大的解决方案空间使得SLM很难生成有效的解决方案。使用单一动作类型的现有基于MCTS的方法限制了多样性,并且很难跨任务泛化。例如,自我一致性(Self-Consistency, SC)方法使用随机采样确保多样性,但SLMs经常产生质量较差的解决方案,需要多次尝试才能找到正确的解决方案,从而增加了推理成本。
其次,准确奖励每个动作是具有挑战性的。没有真实标签,很难验证每个中间步骤si和最终答案sd的正确性。自我一致性中的多数投票要求大多数轨迹是正确的,这通常对于SLMs来说并非如此。像RAP这样的方法使用自我奖励,但我们的研究表明SLMs的表现接近随机自我奖励。像M*(《Mindstar: Enhancing math
reasoning in pre-trained llms at inference time》)中那样训练奖励模型可以解决这一挑战,但在收集训练数据和跨不同任务泛化方面面临困难。
3.2 使用MCTS ROLLOUT自生成推理轨迹
MCTS生成的核心在于动作空间,它定义了树探索的范围。大多数基于MCTS的方法使用单一动作类型构建树。例如,在RAP中,动作是提出下一个子问题,而在AlphaMath和MindStar中,动作是生成下一个推理步骤。然而,依赖单一动作类型很容易导致无效的空间探索。
为了解决这个问题,我们重新审视了人类如何进行推理。不同的人使用不同的动作解决问题:一些人将其分解为子问题,其他人直接解决,有些人可能会重新表述问题以专注于关键条件。此外,人们会根据当前状态调整他们的方法,需要时选择不同的动作。受此人类推理过程的启发,我们引入了更丰富的5种动作,以最大化SLM正确解决复杂推理问题的潜力。
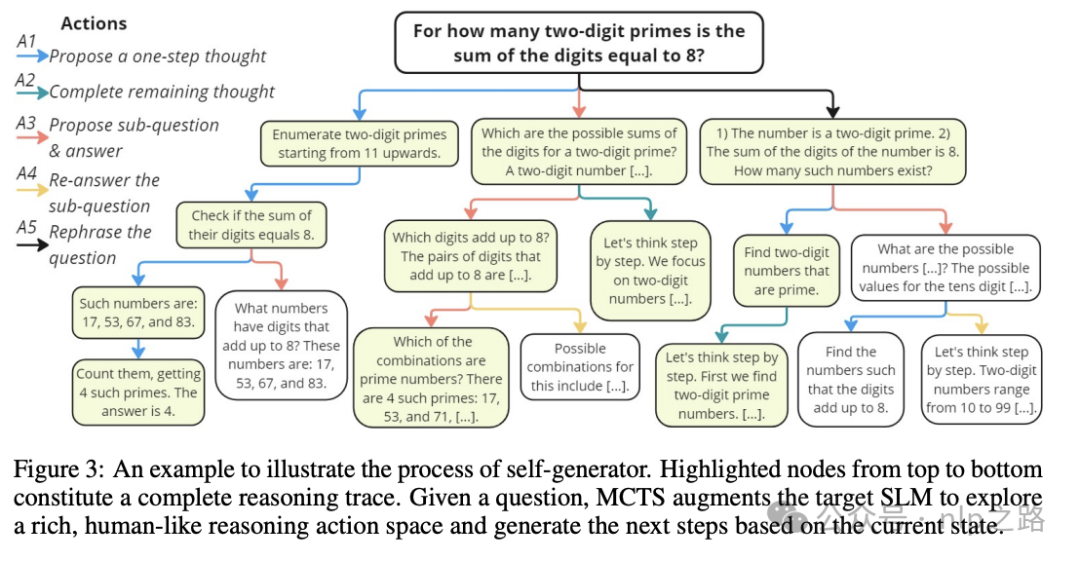
A1:提出一个单步思考。这个动作提示LLM为给定问题生成下一个单步思考,通过考虑现有的推理步骤。与CoT不同,它简化了推理过程,允许LLM进行更好的决策。
A2:提出剩余的思考步骤。这个动作与标准CoT一致,使得“快速思考”能够在较少的步骤中解决简单问题。给定已经生成的推理步骤,它提示LLM直接产生直到达到最终答案的剩余步骤。
A3:提出下一个子问题及其答案。这个动作受到最小到最大提示(least-to-most prompting)的启发,它将复杂问题分解为一系列更简单的子问题并依次解决它们。按照RAP的实现,我们提示LLM提出然后回答下一个子问题。
A4:再次回答子问题。考虑到子问题可能没有被A3正确回答,我们提出了这个动作来重新回答它。为了提高准确性,这个动作提示LLM使用少数样本CoT。注意,A3生成的原始答案没有使用类似CoT的提示,而是遵循最小到最大问题分解提示。
A5:重新表述问题/子问题。在分析错误案例时,我们发现许多是由于LLM误解了问题。例如,它可能错过了问题中提供的一个特定条件。因此,我们提出了一个新的动作来更简单地重新表述问题。具体来说,我们提示LLM清晰地列出问题陈述中给出的所有条件。
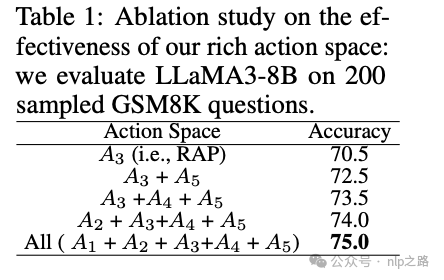
消融实验证明了多样化动作空间,5个动作都用上,效果是最好的。当然上述部分动作之间有先后关系,如A4只能在A3后,A5只能在根节点的问题之后。state是思维树空间的搜索轨迹。
奖励函数:MCTS中的另一个关键组成部分是奖励函数,它评估每个动作的价值并影响了树搜索的方向。我们为SLM设计了一个简单但有效的奖励函数。首先,由于SLM的能力有限,我们排除了任何中间节点的自我奖励技术。其次,为了确保跨推理任务的泛化性,我们避免引入外部监督(例如,外部工具--如计算器--或训练的价值模型)。我们的方法从AlphaGo中汲取灵感,我们根据其对最终正确答案的贡献来评分每个中间节点。因此,经常导致正确答案的动作会获得更高的奖励,使它们在未来的MCTS树扩展中更有可能被选择。
我们定义Q(s, a)为在动作a下生成的节点s的奖励值。最初,所有未探索的节点都被分配Q(si, ai) = 0,导致随机树扩展。在达到第一个终端节点nd时,我们根据是否达到正确答案计算奖励分数Q(sd, ad)。然后,这个分数被反向传播到轨迹t = x ⊕ s1 ⊕ s2 ⊕ ... ⊕ sd中的每个中间节点。具体来说,对于每个si(对于i = 1, 2, ..., d − 1),其Q值更新如下:Q(si, ai) = Q(si, ai) + Q(sd, ad)。为了计算终端节点的Q(sd, ad),我们使用自我一致性多数投票的似然(置信度)作为奖励值。
使用MCTS ROLLOUT生成解决方案:我们现在描述我们的MCTS如何生成候选推理轨迹。从初始根节点s0开始,我们执行多个搜索,包括选择、扩展、模拟和反向传播。具体来说,模拟是使用默认的rollout策略执行的,为了获得更准确的奖励估计,我们执行多个rollout。为了平衡探索和利用,我们使用众所周知的应用于树的上置信界限(Upper Confidence Bounds applied to Trees, UCT)来选择每个节点。这种选择过程在数学上表示为:
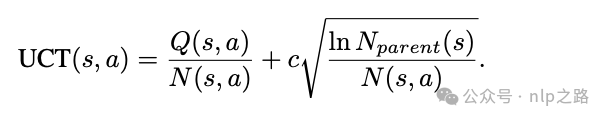
其中N(s, a)是节点s在先前迭代中被访问的次数,Nparent(s)表示s的父节点的访问次数。Q(s, a)是估计的奖励值,将通过反向传播更新。c是一个常数,用于平衡利用和探索。
一旦搜索达到一个终端节点,无论是一个终端状态还是预定的最大树深度d,我们从根节点到终端节点获得一个轨迹。我们从rollout迭代中收集所有轨迹作为候选解决方案。下一节解释了我们如何验证每一个。
3.3 使用相互一致性进行推理轨迹选择
在传统的MCTS中,通常只选择一条轨迹作为最终解决方案,基于特定指标,例如选择rollout迭代中具有最高奖励的路径。不幸的是,经过尝试各种现有方法后,我们发现很难定义一个可靠地选择包含正确答案的轨迹的单一指标。因此,我们收集所有轨迹,并提出相互推理一致性用于答案选择。
判别器SLM2的相互推理一致性:如图2所示,除了目标SLM 1之外,我们引入了另一个SLM 2作为判别器,为每个候选轨迹提供外部无监督反馈。具体来说,对于t = x ⊕ s1 ⊕ s2 ⊕ ... ⊕ sd,我们从随机抽样的步骤i(i < d)开始mask推理步骤。然后,我们提供早期的推理轨迹t = x ⊕ s1 ⊕ s2 ⊕ ... ⊕ si−1作为提示给 SLM2来完成问题的剩余步骤。由于提供了早期i − 1推理步骤作为提示,我们降低了难度,从而增加了SLM2能够提供正确答案的可能性。如下图所示,我们比较SLM2完成的答案是否与原始轨迹t一致。如果它们一致,我们认为t是最终选择的有效轨迹。

我们提供一个直观的解释来说明我们方法背后的合理性。类比同行评审,考虑学生在没有教师反馈的情况下解决问题。一个不确定自己解决方案的学生可能会请同伴审查他们的推理。如果同伴在给定相同的初始步骤的情况下得出相同的答案,学生就会对自己的解决方案更有信心。
SLM1的最终轨迹选择:在对所有候选轨迹应用相互推理一致性之后,我们回到目标SLM 1来从验证过的轨迹中选择最终轨迹。我们通过将每个轨迹的奖励与rollout获得的终端节点的置信度分数相乘来计算每个轨迹的最终分数。选择具有最高最终分数的轨迹作为解决方案。
4 实验